[10000印刷√] 積分 面積 マイナス なぜ 258758-積分 面積 マイナス なぜ

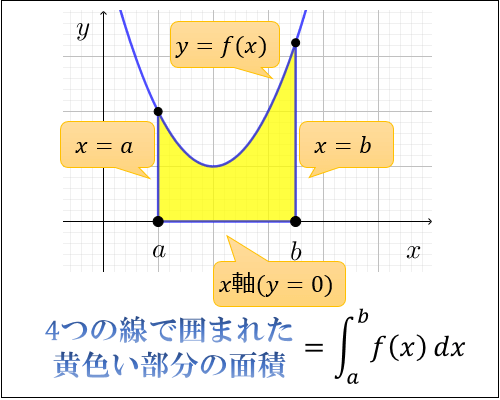
 積分の微分 積分を微分したら元に戻るんじゃないの？ そう思った人はその通りです。 微分の逆として考えたのが積分 でしたものね。 ですが今扱いたいのは 「定積分」の「微分」 です。 定積分は面積と関わりがありましたがこれを微分したら何が起こるのでしょうか。 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 （半径 × 半径 × 円周率 π ）という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さいなぜ定積分で面積が求まるのか そもそも、なぜ定積分をすると面積が求まるのでしょうか？ また、定積分の意味するところは何なのでしょうか？ つまり、 \(y=f(x)\) \(x=a\) \(x=b\) \(x\) 軸 で囲

積分の問題でなぜかマイナスになる面積 19年04月05日のその他のボケ ボケて Bokete

積分 面積 マイナス なぜ

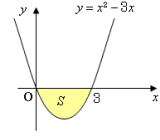
積分 面積 マイナス なぜ- マイナスかけるマイナスはなぜプラスになるのかな？？ 中学数学を勉強し始めて最初にぶつかる壁があります。それは、 マイナスかけるマイナスはなぜプラスになるのか？？ ということです。ゼロより小さいマイナスの数をかけたら、なぜ計算の答えが なんと 面積を計算したはずが値がマイナスになってしまった ではありませんか。 そうなのです。定積分の性質上このように \(x\) 軸よりも下にある面積はマイナスで出てきてしまう のです。 これはどう回避したらいいでしょうか。面積がマイナスはあり得ませんし、そもそも計算として成立しているのか心配ですよね。

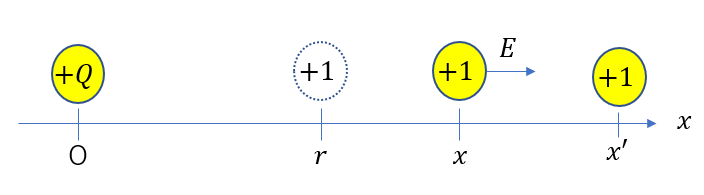
万有引力の位置エネルギーにマイナスがつく理由を分かりやすく解説 受験物理 Set Up

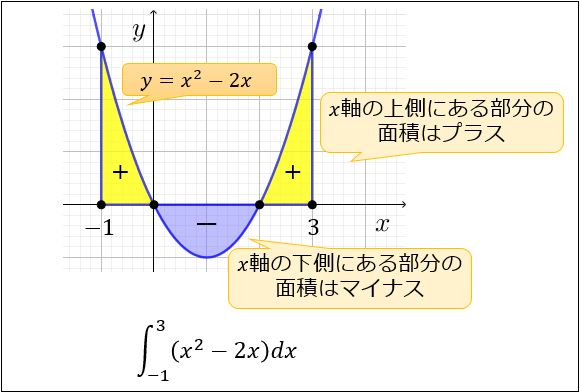
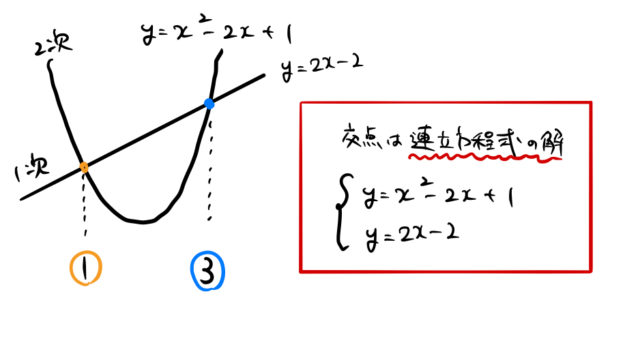
 積分 面積 マイナス なぜX軸の下側の部分の面積はマイナス ∫ − 1 3 (x 2 − 2 x) d x は、下図の 黄色い部分の面積 から 青い部分の面積 を 引いた値 を求めることを意味します。 実際に計算してみると、 ∫ − 1 3 (x 2 − 2 x) d x = 4 3 と求まります。積分は面積を求めるわけではない。 積分を利用Перевод контекст "プラスマイナス" c японский на русский от Reverso Context プラスマイナス数親等そこで，定積分より面積Sを計算すると， のように値が負になってしまいました。 この原因は，積分区間において， f (x)≦0であるのに，そのまま積分してしまった ことです。 誤りは 区間 0 ≦ x ≦ 3 において， x2 3 x ≦ 0 であるのに，そのまま積分してしまったこと 正しくは 区間 a ≦ x ≦ b において，常に f ( x) ≦ 0 のときは， となることを利用する

 マイナスには注意 してください。これはまさしく 1/6 公式が使える形です。 つまり 二次関数と x 軸が囲む面積は必ず 1/6 公式を使える形になる のです。なぜなら交点を出す式が必ず積分をする関数とほぼ同じになるからですね。積分とは何なのか？面積と積分 分数の割り算はなぜひっくり返してかけるのか？その理由を説明する3 つの教え方逆数をかける理由 09m件のビュー;つまり，「微分の逆の操作」を積分と定義する流儀です。 2：「定積分は面積」 y = f (x) y=f(x) y = f (x) と x = a, x = b, x x=a, x=b, x x = a, x = b, x 軸で囲まれた部分の面積（ x x x 軸の下側にある部分の面積はマイナスとする）を ∫ a b f (x) d x \displaystyle\int_a^bf(x)dx ∫ a b f (x) d x と定義する流儀で

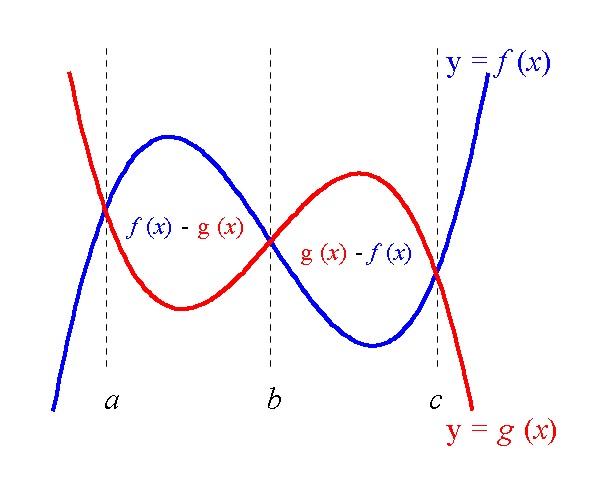
 ある条件のとき、面積や体積を表すことがある、のです。 そして面積や体積でも、計算の上では負となることがあります。 数学では符号つき面積が有効なこともあります。 入門のうちは積分≒面積・体積でもいいかもしれません。(1) 積分で面積を求めるうえで，重要なのは関数の上下と 交点の 座標の 2 つです。 まずはグラフをかいて面積を求める図形と， 2 つの関数でどちらが上に位置するかを把握しましょう。 面積を求めるのは灰色の部分ということがわかります。ここでは が の 上に位置しているので，面積の公式 微分の面積の問題でマイナスにするときとしないときの違いがわかりません！∫a,bf(x)dx = ∫b,af(x)dx って式がありましたよね。積分は、積分変数を走査する方向で正負が変わってしまいます。このため、積分で得られる「面積」は正負

基本 曲線とx軸の間の面積と積分 なかけんの数学ノート

積分とは何なのか 面積と積分計算の意味 アタリマエ

 注意したいのは、 積分範囲と積分する式が公式のような関係になっていないといけない ことと、 右辺には"‐"がつく ことです。まあ面積を求める問題の解きは答えがマイナスになることは無いのでそこで気が付くと思います。1/10 平成23 年6 月1 日午後4 時33 分 07 ストークスの定理：線積分と面積分 安江正樹＠東海大学理学部物理学科 07 ストークスの定理：線積分と面積分 ストークスの定理はガウスの定理とともに、非常に重要な定理であり、線積分と面積分のПеревод контекст "マイナス" c японский на русский от Reverso Context 四半期マイナス, マイナスな人間だな, マイナス面も理解すべきと私は思います, プラスとマイナス, マイナス値

積分の面積公式を分かりやすく解説 まず理解して覚えよう 大学生の勉強部屋

裏ワザ 積分せずに面積を一瞬で求める 6分の1公式 3分の1公式 12分の1公式 とは 使い方をて解説 ますますmathが好きになる 魔法の数学ノート

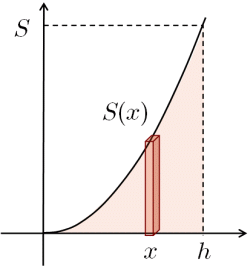
考え方 上の図のように $y=f(x)$ と $x$ 軸で囲まれた部分の $x$ 座標が $a$ から $x$ までの区間の面積を $x$ の関数として $S(x)$ とおきます． 区間を $a$ から $xh$ までにすれば，面積は $S(xh)$ となるはずです． 上の2つの図の面積の差 $S(xh)S(x)$ を考えます． (ⅰ) $h>0$ のとき $S(xh)S(x)$ は当然図の赤い部分になるはずです．区間が $x,xh$ での $f(x)$ の最小値を 積分とは何なのか？面積と積分計算の意味 部分積分の解き方とコツ。どっちを微分するか判断するポイントとは？ 検索 プロフィール 運営者：遠田祐人 統計ライタ―。不動産会社役員。統計解析部門部長。 このサイトでは「1積分法 = すごい足し算 結論から言えば, 積分法は足し算に極限の要素を加えたものと思ってもらって構わない例えば下図のような関数 \( f(x) \) が与えられており, \( f(x) \) と \( x \) 軸, \( x=a \), \( x=b \) によって囲まれた部分の面積を求めよう 以下の議論を始めて見る人にとっては敷居が高く

積分とは何なのか 面積と積分計算の意味 アタリマエ

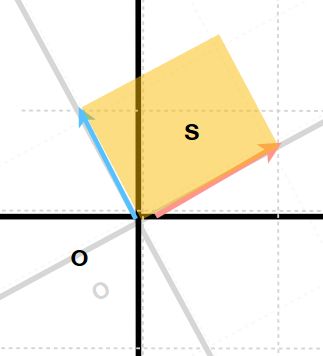
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学

・どうして、点電荷の 電位 の式に、マイナスが付くのですか？ ・電位の基準を、 無限遠点 にとるのはなぜ ？ この疑問をもつ人は、あなただけではなく、物理をやったことがある人すべてに共通する疑問なのです。 そこで今回は、公式の丸暗記をしないで、点電荷の作る 電位 について詳し�7 積分関数と不定 ─138 8 面積・昔と今 ─ 12 マイナス はなにか 8 13 絶対値とは ─210 14 デカルトのかけ算 ─212 15 マイナ スかける はなぜプラ ？ 214 16 分 数と小 ─216 17 半端を表す ─218 18 比率を表す ─2 19 かけ て小さ くなる、わっ 大き ─222 1 2 ＋ 1 3 ＝ 2 5 はどうして いけな積分の計算法について 1 積分の定義 いま, R 上の関数f R → R が, 勝手にひとつ与えられているとします このとき, a,b ∈ R をa < b となる実数として, 関数f(x) の区間a,b 上での積分の値 ∫ b a f(x)dx とは, 皆さん良くご存知のとおり, 区間a,b 上で関数f(x) のグラフとx 軸に囲まれた

速度と加速度とは 定義と求め方 V Tグラフまで徹底解説 受験スタイル

数学定積分で答えがマイナスになることがありますが なぜですか 定 Yahoo 知恵袋

SketchUp is a premier 3D design software that truly makes 3D modeling for everyone, with a simple to learn yet robust toolset that empowers you to create whatever you can imagine積分を行うと、とても複雑で量も多い計算を強いられることが多くあります。 積分は面積を求める方法として有用であり、「面積を求めるには積分を行えば良い」ということは知識として身につけておかなければなりません。 しかし、そもそも定積分するとなぜ面積が求められるのでしょうか？ 今回はこの問いに対して答えていきたいと思います。 準備 広義積分の計算方法とその理解の仕方～そんな計算していいの？ ？ ～ 解析学A (1変数の微積分)や解析学B (多変数の微積分)では、「広義積分」と呼ばれる内容を学習することになります。 「広義」とありますが、これは「広い意味での」ということです

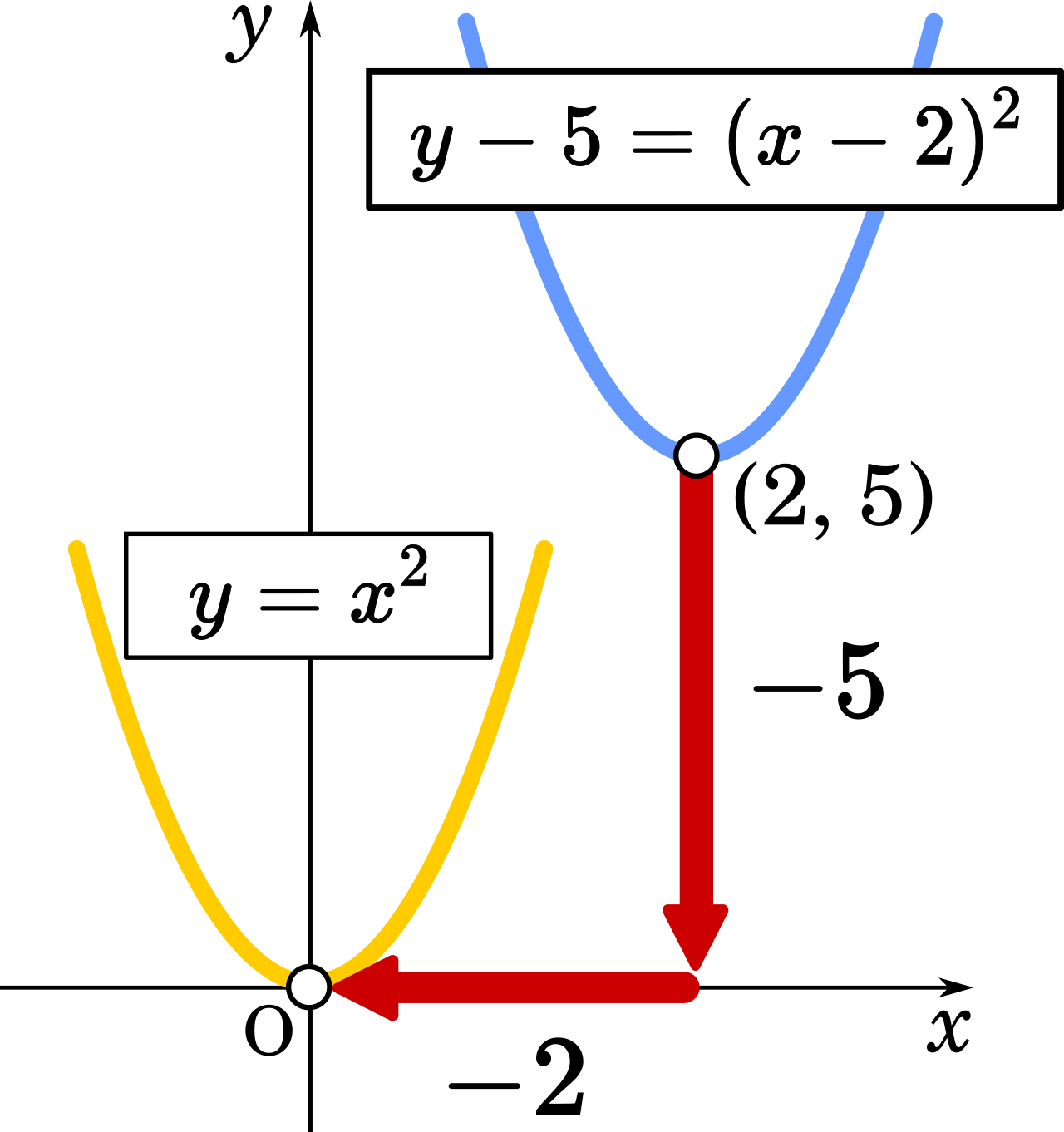
数 二次関数 平行移動の符号はなぜ反対になるのか 答えは見方が逆だから Mm参考書

何故面積はマイナスにならないのですか Quora

曲線を a, bの範囲で積分したものは緑っぽい部分の面積から赤い部分の面積を引いたものになります。 曲線とt軸とで囲まれた面積を普通に考えるとプラスになりますが、図のように赤い部分の面積のほうが大きいと積分した値はマイナスになります。 これは赤い部分の面積がマイナスだからと捉えることが出来ます。 例2） 球体からそれよりちょっと半径の 面積分で出た値って負になることあるんですか？正になることも負になることもよくあります。面積分が実際の問題で出てくる場合、被積分関数はベクトル場であって、lim Σ F・ n ΔSのような形で登場するのが普通です。さらに、面には向きが積分は「無限個の長方形に分割する」という考え方（区分求積法）を使っている。 区分求積法で面積を表すためには、 一定区間を h 分割し、 幅 \frac {1} {h} の長方形の面積を、それぞれ文字で表し、 その総和をシグマで表現し、 h を h\to \infty とし、無限

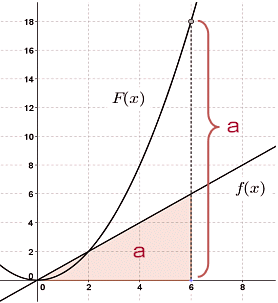
積分 なぜ積分で面積が求められるのか 大人が学び直す数学

マクスウェル方程式 電磁気学まとめ

定積分の計算には，そのうちどれか1つの原始関数を用いればよいが，計算が簡単なように C=0 となるものを用いる． すなわち， n F (x) C = (F (b) C )− (F (a) C )=F (b)−F (a) となり，どんな C の値を用いても差で消えるので，計算が最も簡単になる C= 0 の場合を用いる． なぜ原始関数を使うのか，なぜ差なのか，そんなことをして何になるのか （教科書の項目として連絡先 kantaro@momosonetnejpツイッター http//twittercom/Kantaroお勧め動画自然対数の底e ネイピア数を東大留年美女＆早稲田 wha******** wha******** さん 12/7/16 2（編集あり） 補足後 微小な長方形の面積を集める算法が積分です。 つまりlimΣΔyΔxを計算しています。 ΔyとΔxの符号の付け方で如何様にも変わります。 * 正にもなれば、負にもなります。 当然、ZEROにもなります。 第一、第三象限は正になり、第二象限、第四象限は負になります

3

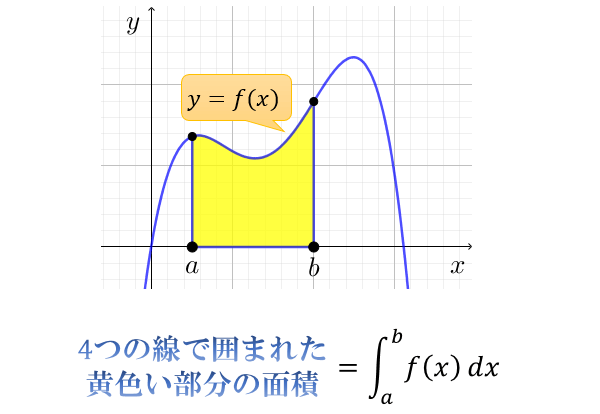
積分とは何なのか 面積と積分計算の意味 アタリマエ

1 第1章 基礎事項 11 微分積分 偏微分 変数x, y, z の関数f = f(x,y,z)について ∂f ∂x) yz = lim ∆x→0 f(x∆x,y,z)−f(x,y,z) ∆x (11) をf のxによる1階の偏微分という y, z による偏微分についても同様に 定義する ここで, 左辺の()につけた添え字yz は偏微分を行うさいにy, z を一定とみなすことを意味するなぜ積分で面積を計算するのか？ 積分を使って面積の求め方を説明しました。例題にした「四角形の面積」では、積分のメリットを感じられなかったと思います。 積分を使った面積の算定で、最大のメリットは、 任意断面の面積が計算できる ことです。下図をみてください。任意断面の面積は計算が困難です。公式もありません。しかし、四角形の微小面積dAを合計 積分をしていく途中で \dfrac16 公式の形が出たら使えるというだけであって、面積を求めるときでなくても当然使えます。なぜか面積のときにしかこの公式を使おうとしない人がいますが、そのようなことはありません。 まとめると、

楕円の知識まとめ 面積 方程式 焦点 接線 媒介変数表示 理系ラボ

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

 積分値のはピークの面積だからです。線幅が広い場合はピークの高さが小さくても面積は大きい場合があります。 積分値の見方 重水素(d)は観測されない（ここでは化学シフト値は気にしないでいい） ここでは大きいものが4

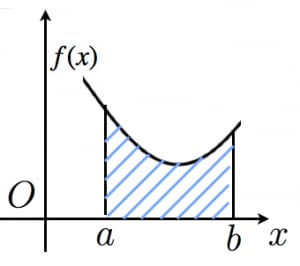
なぜ定積分で面積が求まるのか 高校数学の美しい物語

楕円の知識まとめ 面積 方程式 焦点 接線 媒介変数表示 理系ラボ

理系のための 微分 積分復習帳 高校の微積分からテイラー展開まで ブルーバックス 竹内淳 数学 Kindleストア Amazon

勉強しよう数学 積分可能の定義と原始関数と不定積分の求め方

高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

高校数学について 積分における6分の1公式ってなぜマイナス6分の Yahoo 知恵袋

消費者余剰 瞬時に分かる経済学

積分はなぜ面積を表すのか 高校数学 積分法 １９ Youtube

数学定積分で答えがマイナスになることがありますが なぜですか 定 Yahoo 知恵袋

写真が横でごめんなさい これは奇関数ではないのですか 0だと思っ 数学 教えて Goo

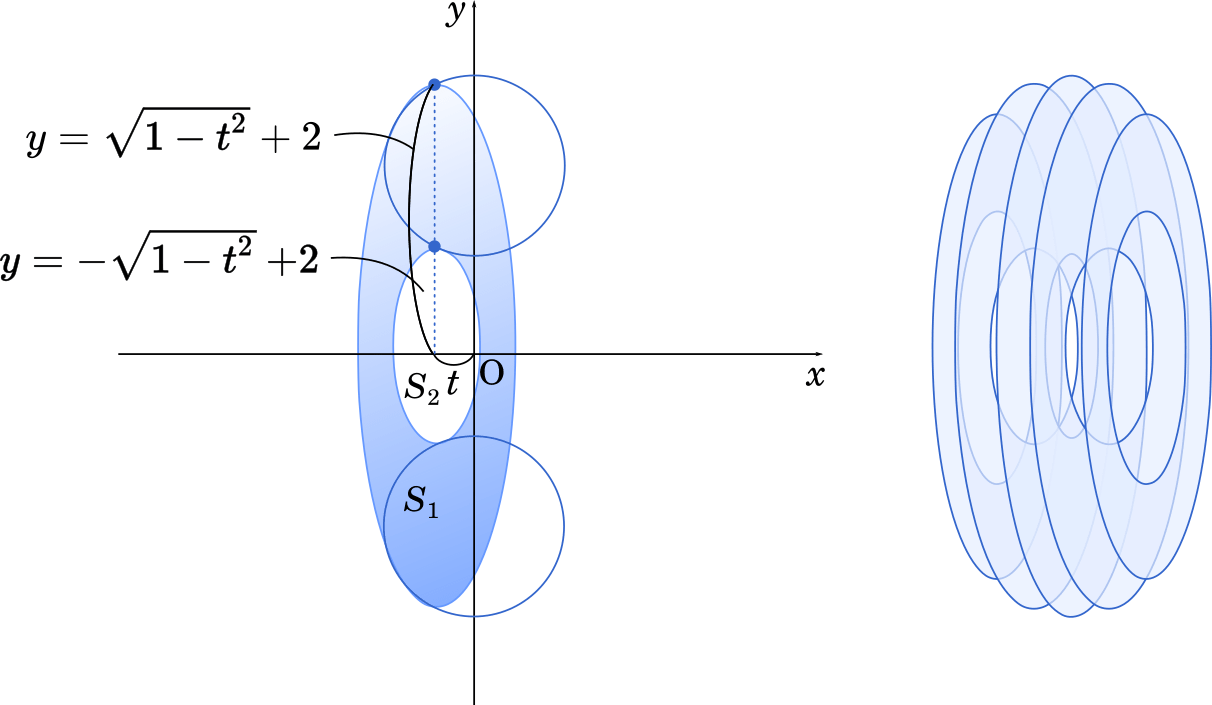
数iii積分 円環体 ドーナツ型 の体積の求め方 Mm参考書

高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

1 12公式 3次関数 おいしい数学

勉強しよう数学 積分可能の定義と原始関数と不定積分の求め方

高校数学 B 積分 公式を使わずに面積を求める方法 やはり俺の考察ブログはまちがっている アニメ 数学

区分求積法 なぜ定積分は面積を表すの 文理どっちでも理解できるよう優しく解説 青春マスマティック

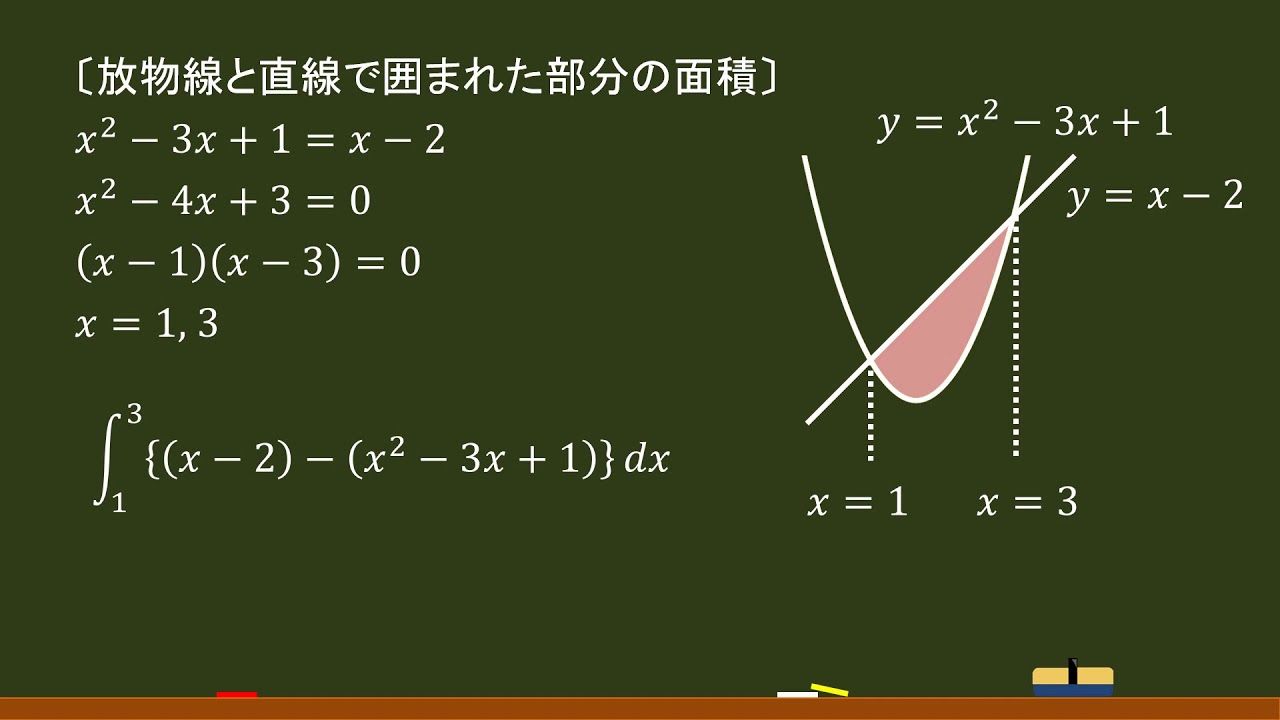
数 積分法 放物線と直線で囲まれた部分の面積 1 6公式の利用 オンライン無料塾 ターンナップ Youtube

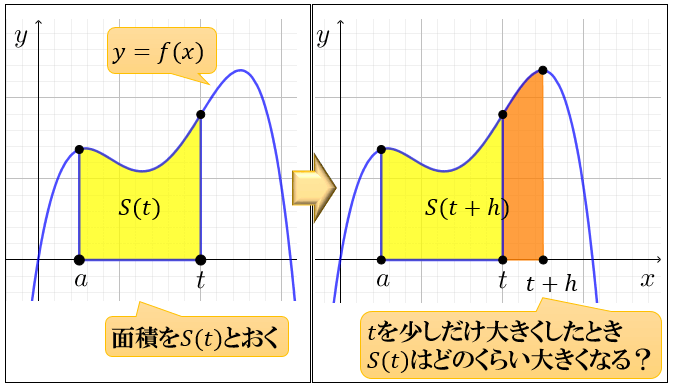
積分とは何なのか 面積と積分計算の意味 アタリマエ

区分求積法 なぜ定積分は面積を表すの 文理どっちでも理解できるよう優しく解説 青春マスマティック

面積公式 6分の1等 をうまく使う方法を解説 数2積分法

基本 曲線とx軸の間の面積と積分 なかけんの数学ノート

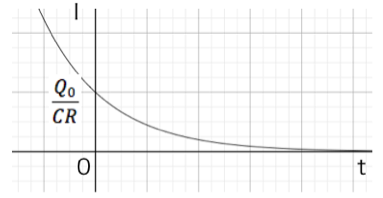
なぜ電流を積分すると電気容量が求められるのか 微積で物理 科学のネタ帳

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

なぜ定積分で面積が求まるのか 高校数学の美しい物語

定積分 面積がマイナス Youtube

新入社員よ 覚えておこう 仕事の評価は微分積分で決まる ニュースイッチ By 日刊工業新聞社

なぜ球の体積は Math Frac43 Pi R 3 Math なのでしょうか Quora

マイナスかけるマイナスはなぜプラスか

積分とは何なのか 面積と積分計算の意味 アタリマエ

定積分 疑問 定積分 疑問定積分の値が負の値になることはあります 数学 教えて Goo

積分の問題でなぜかマイナスになる面積 19年04月05日のその他のボケ ボケて Bokete

高校数学 X軸周りの回転体の体積 V P Y Dx 受験の月

虚数はなぜ人を惑わせるのか 朝日新書 竹内 薫 本 通販 Amazon

新入社員よ 覚えておこう 仕事の評価は微分積分で決まる ニュースイッチ By 日刊工業新聞社

Newtonライト 虚数のきほん ニュートンプレス

1 6公式の使い方 思考力を鍛える数学

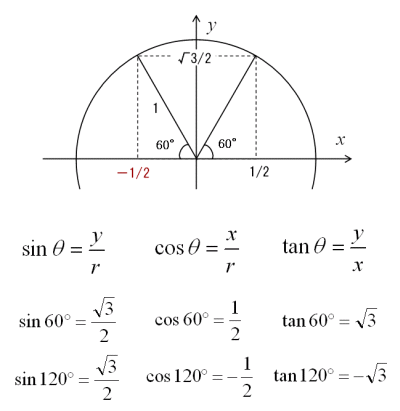
三角比 鈍角の三角比 大人が学び直す数学

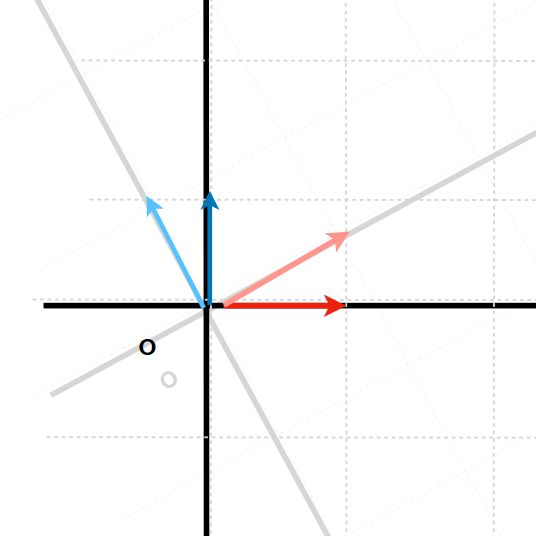
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学

万有引力の位置エネルギーにマイナスがつく理由を分かりやすく解説 受験物理 Set Up

積分の面積公式を分かりやすく解説 まず理解して覚えよう 大学生の勉強部屋

めもめもーめもblog 外積の計算のマイナス項の意味 直感的理解を目指して

物理のヒント集 ヒントその３ ｖ ｔグラフでの面積と変位の関係 日々是鍛錬 ひびこれたんれん

符号付きの面積ってなに ー定積分で面積がマイナスになる理由 Youtube

微分積分の超初心者に 5時間で攻略する本 レビュー 趣味の大学数学

数学 積分法 怜悧玲瓏 高校数学を天空から俯瞰する

数学の定積分と面積のところがわかりません画像のやつですマイナスがつく式ら Yahoo 知恵袋

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

ネイピア数とは 自然対数の底eについて解説 空間情報クラブ 株式会社インフォマティクス

高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら

3

なぜ積分すると面積が求まるのか あ そんなことか

台形公式について 次の問題で なぜ F X 0ではなく なぜ F X Okwave

Q Tbn And9gcqoe6nsji Rx8v2ojhj51motkq Iaqslrejrf0db8emklcii6qg Usqp Cau

積分 積分でなぜ体積が求められるのか 大人が学び直す数学

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

面積を積分して求めた時に答えがマイナスになってしまったら 面積がマイナスになる訳無 Clear

数学の図形の面積を求める問題でなぜか面積がマイナスになっている 形状へのボケ ボケて Bokete

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

2次元での積分

1 12公式 3次関数 おいしい数学

ここから 方向を含む面積積分の話 Ppt Download

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

F X は関数を積分しているので 面積をあらわすと教わったのですが グラフではxが1 Clear

1 赤で丸印をつけた部分はなぜ 急にマイナスが出てくるのですか Clear

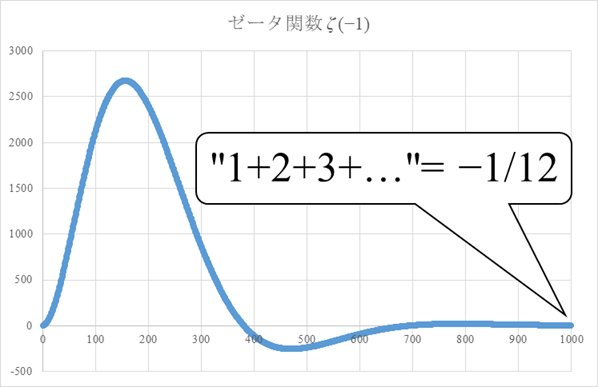
なぜゼータ関数の自然数の和は無限大に発散しないのか

裏ワザ 積分せずに面積を一瞬で求める 6分の1公式 3分の1公式 12分の1公式 とは 使い方をて解説 ますますmathが好きになる 魔法の数学ノート

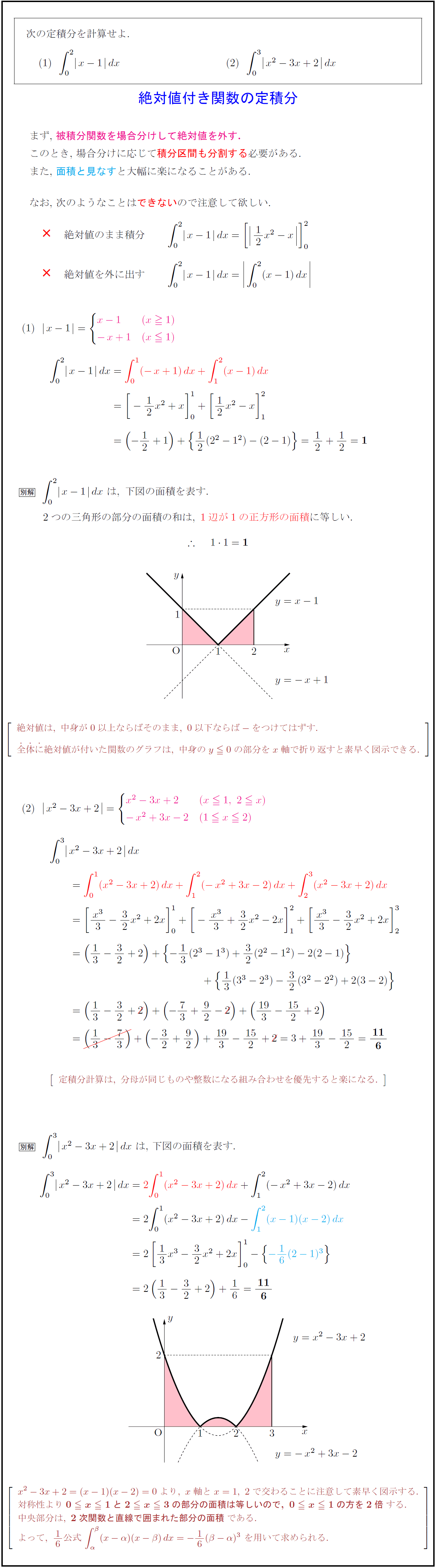
高校数学 絶対値付き関数の定積分 基本 受験の月

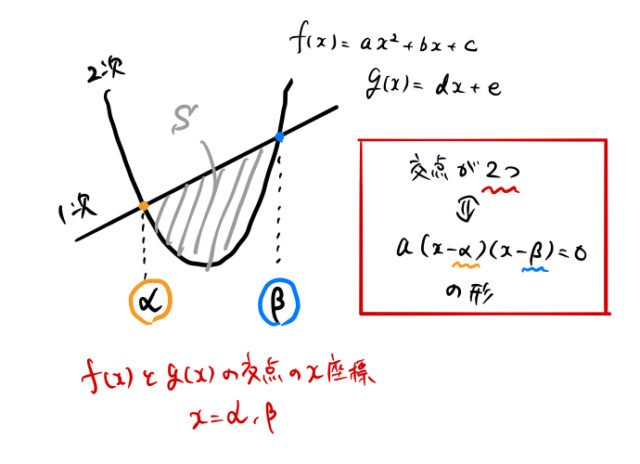
高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら

なぜ定積分で面積が求まるのか 高校数学の美しい物語

微分積分を速度と距離の関係で理解する 自然科学研究会２ 生活の中の数学 その２

この赤い線の部分の マイナスはなぜつくのでしょうか Clear

数2 定積分の範囲です ぐちゃぐちゃで申し訳ないのですが教えてください Clear

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

ここから 方向を含む面積積分の話 Ppt Download

面積の計算について 数学 苦手解決q A 進研ゼミ高校講座

マイナスかけるマイナスはなぜプラスか

3

48s96ub7b0z5f Net Teisekibun Menseki Kihon

積分 ２つの曲線の間の面積を求める公式の証明 数学ii By ふぇるまー マナペディア

48s96ub7b0z5f Net Rokubunnoichi Koushiki Menseki

微分積分を速度と距離の関係で理解する 自然科学研究会２ 生活の中の数学 その２

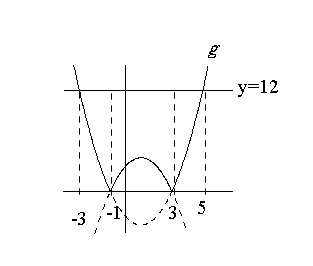
定積分によって面積を求める問題の解き方と公式

台形公式について 次の問題で なぜ F X 0ではなく なぜ F X Okwave

なぜ数式には2乗が多いのか Qiita

偶関数 奇関数とは 意味や見分け方 積分での使い方 受験辞典

X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫

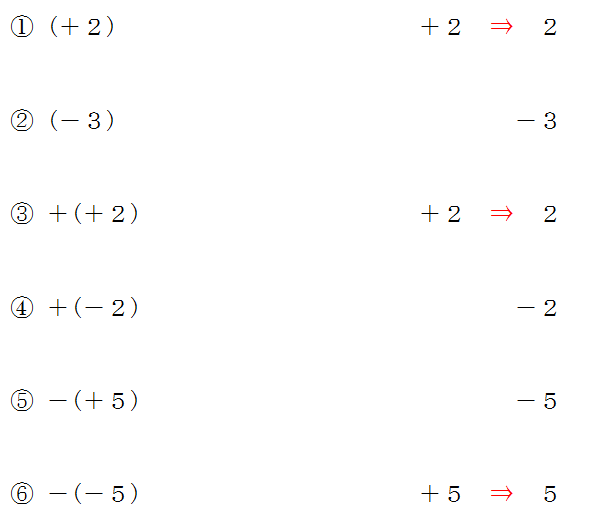
カッコの外し方 カッコの前にマイナスがあると符号がかわる 三重の個人契約家庭教師

定積分によって面積を求める問題の解き方と公式

Incoming Term: 積分 面積 マイナス なぜ,